My current work (no pun intended, but I'll take it anyway) focuses on the development of general relativistic resistive magnetohydrodynamics inspired by 14-moment methods.

The "usual" relativistic hydrodynamics equations are defined by requiring the baryon number density current, \(N,\) and the fluid energy-momentum density, \(T,\) be conserved; i.e., \( \nabla \, \cdot N = 0 \) and \( \nabla \cdot T = 0 \). Since \(N\) is a four-vector and \(T\) is a symmetric (2,0) tensor in four dimensions (and therefore has ten independent components), these two objects comprise 14 degrees of freedom. However, the conservation equations are only five in number. Therefore, this model leads to nine unconstrained degrees of freedom; i.e., nine degrees of freedom without corresponding evolution equations. These nine degrees of freedom correspond to dissipative processes. One option is to set all of these equal to zero; this leads to a (very successful) model of equilibrium hydrodynamics. The 14-moment method provides a means to instead derive evolution equations for these dissipative degrees of freedom.

One nice way to define \(N\) and \(T\) is as the first and second moments of a distribution function, \(f\), which itself describes the number number density of fluid particles in an eight-dimensional phase space comprised of spacetime points \(x\) and four-momenta \(p\). The normalization of \(u\) (i.e., \(u\cdot u=-1\), with \(u:=\dot{x}\)) and \(p\) (i.e., \(p\cdot p = -m^{2}\), with \(m\) the mass of a single particle), lead to the eight-dimensional phase space reducing to a six-dimensional phase space.

More description to come...

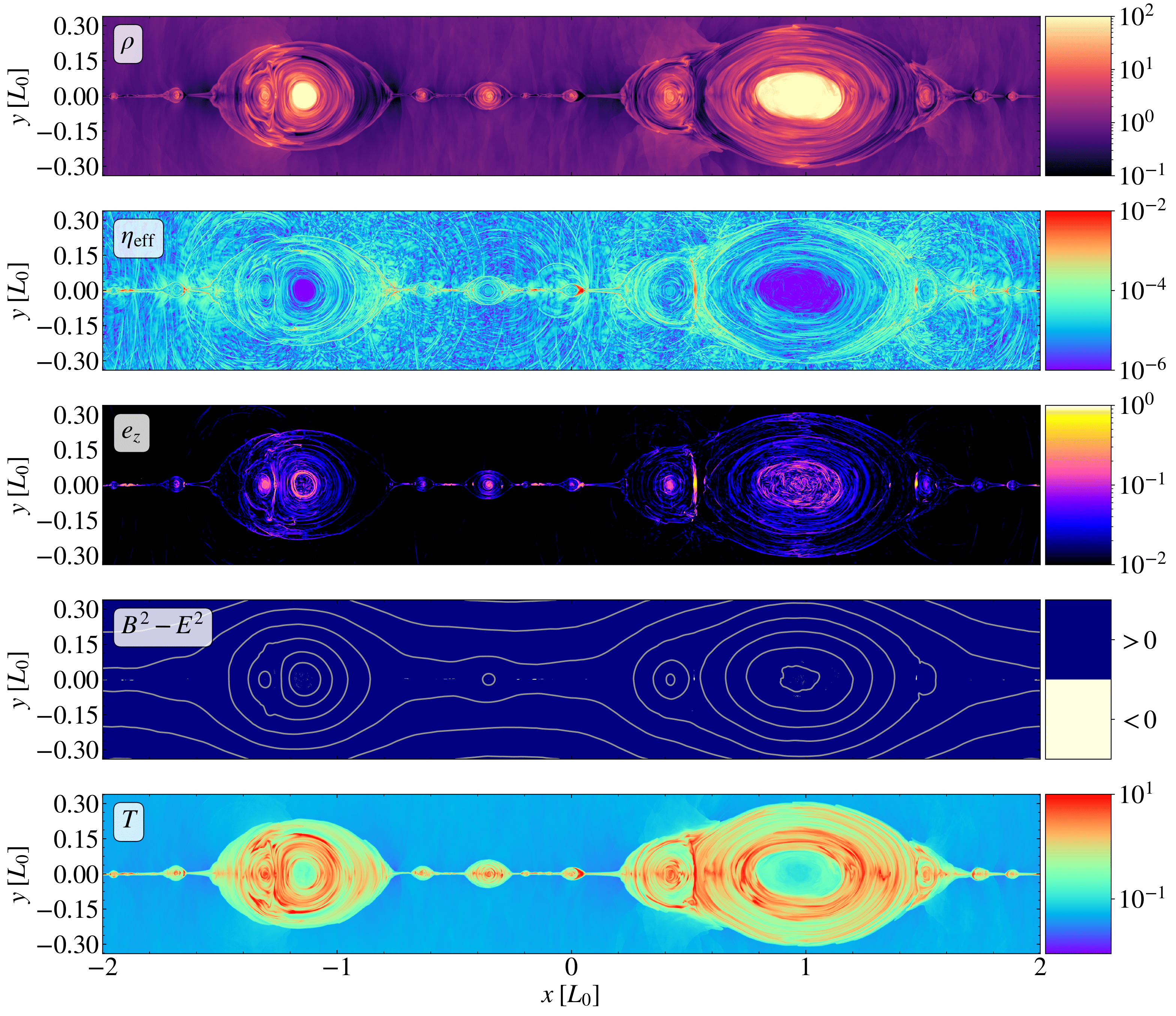
Gorgeous figure showing magnetic reconnection (used with permission) from
Bugli et al., arXiv 2410.20924 (2024)

The stability of stars is due to the inward pull of gravity being balanced by the outward push from gas pressure and radiation pressure produced by nuclear fusion, in addition to pressure support from degenerate electrons in the stellar core. When the core runs out of material to fuse, this balance is lost and material accumulates onto the core unimpeded. Eventually, the core will reach its effective Chandresekhar mass, at which point the electron degeneracy pressure is insufficient to support the core, gravity takes over, and the core begins to collapse. If the star is more massive than about ten Suns, this collapse will end in a spectacular explosion known as a core-collapse supernova, the energy output of which is approximately 100 times that which our Sun will produce in its entire ten million year lifetime! What's more, all that energy is released in a matter of seconds!! These explosions distribute many of the heavy elements in our solar system, including carbon, the element on which life as we know it is based, and so it behooves us to understand this process well, because it is to that which we literally owe our entire existence! Although there are many promising leads, it is not currently known exactly how this explosion proceeds.

What is known is that the core collapses until the pressure is so high that the repulsive electrical forces between the electrons and the nuclei are overcome and the electrons and protons combine to form neutrons (and neutrinos), thus effectively creating a single nucleus the size of a city—this is what will eventually become a neutron star (assuming it doesn't collapse to a black hole). This transition produces a shock wave that propagates outward. It is intuitive that this shock wave simply propagates through the entire star, blowing the material away with it; however, as often happens, nature is not so simple. It was discovered via computer simulations that the shock wave stalls about 200 km from the center of the star. The shock is somehow re-energized, and continues on its explosive path. One goal of supernova models is to determine this re-energization mechanism.

For my PhD, I worked under the guidance of Professors Kelly Holley-Bockelmann at Vanderbilt University, Eirik Endeve at Oak Ridge National Laboratory, and Anthony Mezzacappa at the University of Tennessee at Knoxville on the toolkit for high-order neutrino-radiation hydrodynamics, thornado, a computer code that aims to simulate core-collapse supernovae in three dimensions using Runge–Kutta discontinuous Galerkin methods. My work focused on developing a module that solves the general relativistic hydrodynamics equations under the 3+1 decomposition of spacetime and the conformally-flat condition.

These simulations are computationally very expensive, requiring many hours on leadership-class supercomputers such as Summit and Frontier. To effectively utilize these resources, our code must be able to run in parallel with multiple CPU cores, and also on GPUs. To achieve this, we are coupling thornado to AMReX, a software package designed to allow codes to run in parallel and use block-structured adaptive mesh refinement, allowing us to focus the resources on those parts of the simulation that most need them.

Publications
Dunham et al., ApJ 964:38 (2024)
Pochik et al., ApJS 253:21 (2021)
Pochik et al., ApJS 253:21 (2021)
Dunham et al., J. Phys. Conf. Ser. 1623:012012 (2020)
Endeve et al., J. Phys. Conf. Ser. 1225:012014 (2019)

One consequence of Einstein's theory of general relativity is that as light travels through a gravitational field, it is deflected. This phenomenon is known as gravitational lensing, because the effects are similar to those of light traveling through a lens. For these effects to be measurable, enormous masses are required, e.g., a star, a galaxy, or something even bigger! One source of measurable gravitational lensing is the light from entire galaxies being deflected by the mass of a galaxy cluster, the largest gravitationally-bound objects in the Universe. In analogy with a physical lens, gravitational lenses can also have magnification effects, increasing the apparent size of a galaxy, allowing astronomers to see features that would otherwise be too small to discern.

A special case of gravitational lensing is so-called strong lensing, where the light is deflected to such a degree that multiple light rays leaving the same point, but traveling in different directions, can all be bent directly toward us, causing us to see multiple images of the source (like the mouth and sides of the smiley face in the accompanying picture).

As an undergraduate I did research with Professor Keren Sharon in strong gravitational lensing, as part of the Sloan Giant Arcs Survey (SGAS). My work involved modeling these strong lenses (i.e., clusters of galaxies, two of which make up the eyes of the smiley face in the picture) to determine their masses based on the color, shape, and other properties of the multiple images.

See my undergraduate honor's thesis on one particular lens, SDSS J1438+1454, here, or the published journal article that came out of that research here.